벡터 검색과 ANN(Approximate Nearest Neighbor) 알고리즘은 대규모 데이터셋에서 유사한 항목을 빠르게 찾는 데 필수적인 기술입니다. 본 글에서는 다양한 벡터 검색 인덱스에 대해 소개합니다.
Flat Index
모든 벡터를 직접 저장하며, Brute-Force 방식으로 검색합니다. 데이터셋 내의 모든 벡터를 비교하여 가장 가까운 결과를 반환하기 때문에 구현이 간단하며 정확도가 높습니다.
인덱스 생성
- 벡터의 차원을 설정합니다.
- 모든 벡터를 데이터베이스에 추가하여 저장합니다.
검색 방식
- 쿼리 벡터를 입력합니다.
- 저장된 모든 벡터와 비교하여 가장 가까운 이웃을 반환합니다.
특징
- 장점: 100% 정확한 결과를 반환. 모든 벡터를 비교하기 때문에 가장 가까운 이웃을 항상 정확히 찾습니다.
- 단점: 대규모 데이터셋에서는 검색 속도가 매우 느릴 수 있으며, 메모리 사용량이 높아질 수 있습니다.
- 적합한 경우: 소규모 데이터셋이나 정확도가 최우선인 작업.
Faiss에서
https://github.com/facebookresearch/faiss/wiki/Faiss-indexes#flat-indexes
Milvus에서
https://milvus.io/docs/index.md?tab=floating#FLAT

- nq(쿼리에 대한 대상 벡터의 수)가 증가할수록 쿼리 시간이 늘어납니다.
- Milvus의 FLAT 인덱스를 사용하면 nq가 200을 초과하면 쿼리 시간이 급격히 증가합니다.
- 일반적으로, FLAT 인덱스는 Milvus를 GPU에서 실행할 때보다 CPU에서 실행할 때 더 빠르고 일관성이 있음. 그러나 nq가 20 미만일 때 CPU에서 FLAT 쿼리가 더 빠릅니다.
LSH(Locality-Sensitive Hashing)
벡터를 해시 함수로 변환하여 고차원 데이터를 저차원 해시값으로 매핑하는 방식입니다. 데이터가 가까운 경우 동일한 해시값을 가질 확률이 높아 효율적인 검색이 가능합니다.
인덱스 생성
- 해시 함수의 개수와 파라미터를 설정합니다.
- 데이터셋의 각 벡터를 해시 함수로 변환하여 인덱스에 저장합니다.
- 동일한 해시값을 가지는 벡터들을 클러스터링합니다.
검색 방식
- 쿼리 벡터를 입력합니다.
- 쿼리 벡터를 해시 함수로 변환하여 해시값을 생성합니다.
- 동일한 해시값을 가지는 벡터들만 비교하여 근사 최근접 이웃을 반환합니다.
Faiss에서

nbits 인수는 해시된 벡터의 '해상도'를 나타냅니다. 값이 높을수록 더 많은 메모리와 더 느린 검색 속도 대신 더 높은 정확도를 의미합니다.

- LSH는 더 큰 d 값을 사용할 때 차원의 저주에 매우 민감하므로 검색 품질을 유지하려면 nbits도 늘려야 합니다.
- 저장된 벡터는 원래 벡터 차원 d가 증가함에 따라 점점 더 커집니다. 이는 곧 과도한 검색 시간으로 이어집니다.
- 이는 인덱스 메모리 크기에 반영됩니다.

- 따라서 IndexLSH는 벡터 차원이 큰 경우 적합하지 않습니다(128은 이미 너무 큽니다).
- 대신, 차원이 낮은 벡터와 작은 인덱스에 가장 적합합니다.
Milvus에서
milvus에서는 LSH를 지원하지 않습니다.
HNSW(Hierarchical Navigable Small World)
고차원 벡터 공간에서 효율적인 검색을 제공하는 그래프 기반 알고리즘입니다. 각 벡터는 그래프의 노드로 표현되며, 최근접 이웃을 탐색하는 데 최적화되어 있습니다. 'NSW' 부분은 그래프 내의 모든 정점이 직접 연결되어 있지 않음에도 불구하고 그래프 내의 다른 모든 정점으로 가는 평균 경로 길이가 매우 짧기 때문에 발생합니다.
높은 수준에서 HNSW 그래프는 NSW 그래프를 가져와 여러 레이어로 나누어 구축합니다. 각 증분 레이어는 정점 간의 중간 연결을 제거합니다. 차원성이 더 높은 더 큰 데이터 세트의 경우 HNSW 그래프는 우리가 사용할 수 있는 가장 성능이 좋은 인덱스 중 일부입니다. HNSW 인덱스만 사용하여 다루겠지만, 다른 양자화 단계를 계층화하면 검색 시간을 더욱 개선할 수 있습니다.

인덱스 생성
- 각 벡터를 그래프의 노드로 추가합니다.
- 노드 간 연결을 설정하며, 연결 수(M)를 지정합니다.
- 탐색 효율성을 높이기 위해 계층적 그래프 구조를 생성합니다.
검색 방식
- 쿼리 벡터를 입력합니다.
- 검색은 그래프의 최상위 계층에서 고정된 입구 지점(사전에 정해진 노드)에서 시작됩니다.
- 알고리즘은 현재 계층에서 쿼리 벡터에 가장 가까운 이웃으로 greedy하게 이동하며, 더 이상 쿼리 벡터에 가까이 갈 수 없을 때까지 진행됩니다. 상위 계층은 탐색 목적의 거친 필터 역할을 하여 하위 계층에서 세부적인 검색을 위한 잠재적인 입구 지점을 찾도록 도와줍니다.
- 현재 계층에서 지역 최소값(local minimum)에 도달하면, 알고리즘은 사전에 설정된 연결을 사용하여 하위 계층으로 이동하고 탐욕적 검색을 반복합니다.
- 이 과정은 최하위 계층에 도달할 때까지 계속되며, 마지막으로 최종 정제 단계에서 가장 가까운 이웃을 식별합니다.
- 결과를 반환합니다.
특징
- 장점: 높은 검색 속도와 정확도를 동시에 제공합니다. 검색 경로를 줄이는 효율적인 탐색 구조를 사용합니다.
- 단점: 메모리 사용량이 많으며, 그래프를 구성하는 데 시간이 소요될 수 있습니다.
- 적합한 경우: 중대규모 데이터셋에서 정확성과 속도가 모두 중요한 경우.
Faiss에서
https://github.com/facebookresearch/faiss/wiki/Faiss-indexes#indexhnsw-variants
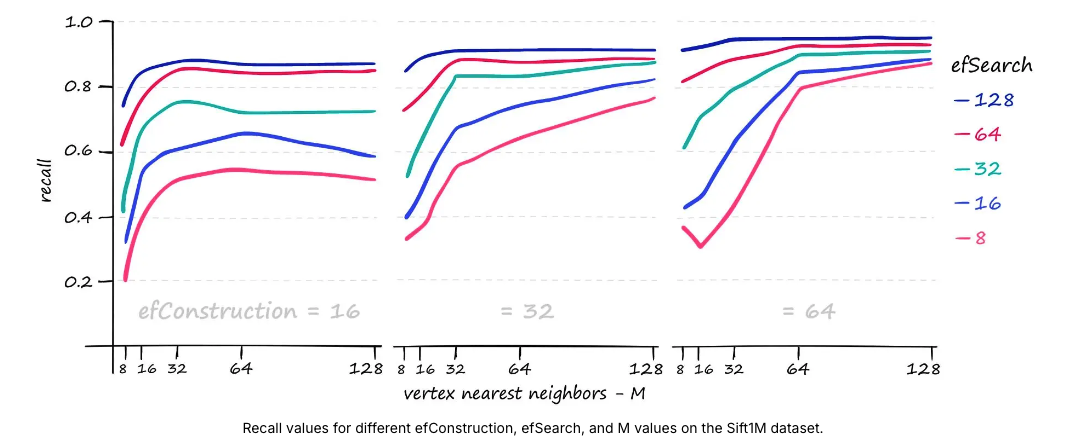
- M — 각 정점이 연결할 가장 가까운 이웃의 수입니다.
- efSearch — 검색 중에 레이어 사이에서 몇 개의 진입점을 탐색할 것인가.
- efConstruction — 인덱스를 구축할 때 탐색할 진입점의 수입니다.
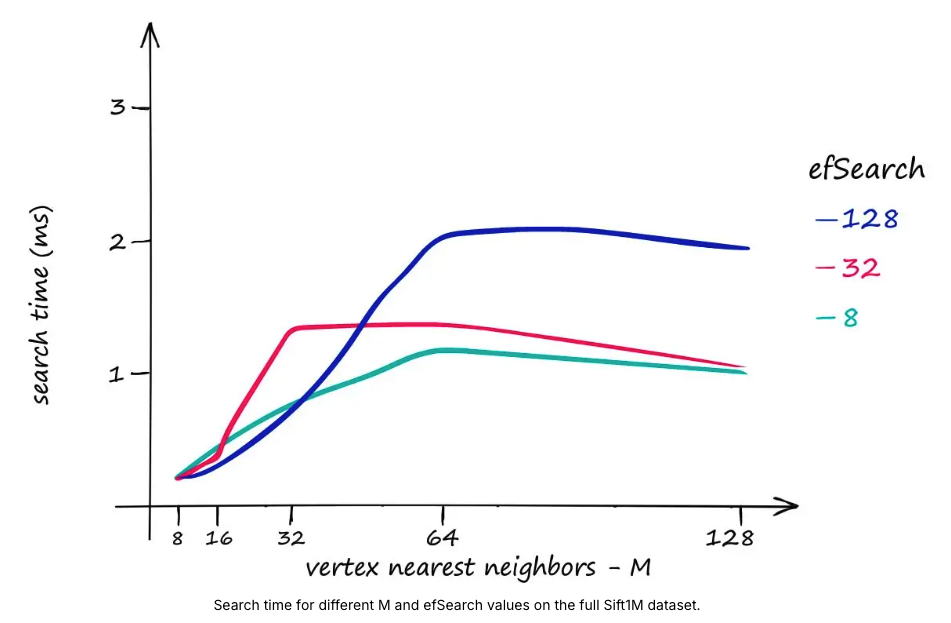
- M과 efSearch는 검색 시간에 더 큰 영향을 미칩니다.
- efConstruction은 주로 인덱스 구성 시간을 증가시킵니다(즉, index.add가 더 느려짐).
- 하지만 더 높은 M 값과 더 높은 쿼리 볼륨에서는 efConstruction이 검색 시간에 미치는 영향도 확인할 수 있습니다.

- HNSW는 매우 빠른 검색 속도로 뛰어난 검색 품질을 제공하지만, HNSW 인덱스는 상당한 양의 메모리를 차지합니다.
- Sift1M 데이터 세트에 M 값 128을 사용하려면 1.6GB 이상의 메모리가 필요합니다.
- 인덱스 메모리 공간에 영향을 주지 않고 다른 두 매개변수인 efSearch와 efConstruction을 늘릴 수 있습니다.
- RAM이 제한 요소가 아닌 경우 HNSW는 세 가지 매개변수를 늘려 품질에 더욱 집중할 수 있는 균형 잡힌 지수로서 매우 좋습니다.
Milvus에서
https://milvus.io/docs/index.md?tab=floating#HNSW
https://milvus.io/docs/hnsw.md
- M 값에 대한 권장 사항
- M 값을 증가시키면 일반적으로 정확도가 높아지지만, 메모리 사용량이 증가하고 인덱스 빌드 및 검색 속도가 느려집니다.
- M 값을 증가시키는 것을 고려해야 할 경우: 데이터셋의 차원이 높거나 높은 재현율(recall)이 중요한 경우.
- M 값을 감소시키는 것을 고려해야 할 경우: 메모리 사용량 및 검색 속도가 주요 우선사항인 경우.
- 권장 범위: 대부분의 경우 [5, 100] 사이의 값을 설정하는 것을 추천합니다.
- efConstruction 값에 대한 권장 사항
- efConstruction 값을 증가시키면 더 많은 잠재적 연결을 탐색하므로 인덱스의 정확도가 향상됩니다. 그러나 이로 인해 인덱스 빌드 시간이 길어지고, 빌드 중 메모리 사용량이 증가합니다.
- efConstruction 값을 증가시키는 것을 고려해야 할 경우: 정확도를 개선해야 하며, 인덱싱 시간은 덜 중요한 경우.
- efConstruction 값을 감소시키는 것을 고려해야 할 경우: 자원 제한으로 인해 인덱스 빌드 속도를 높여야 하는 경우.
- 권장 범위: 대부분의 경우 [50, 500] 사이의 값을 설정하는 것을 추천합니다.
- ef 값에 대한 권장 사항
- ef 값을 증가시키면 더 많은 잠재적 이웃을 고려하므로 검색 정확도가 향상됩니다. 그러나 검색 시간이 증가합니다.
- ef 값을 증가시키는 것을 고려해야 할 경우: 높은 재현율(recall)을 달성하는 것이 중요하며, 검색 속도는 덜 중요한 경우.
- ef 값을 감소시키는 것을 고려해야 할 경우: 검색 속도를 우선시하며, 약간의 정확도 감소가 허용 가능한 경우.
- 권장 범위: 대부분의 경우 [K, 10K] 사이의 값을 설정하는 것을 추천합니다.
IVF (Inverted file)
데이터셋을 여러 클러스터로 나누어 검색 영역을 줄이는 방식입니다. 검색 시 특정 클러스터만 확인하므로 속도가 크게 향상됩니다.
인덱스 생성
- 데이터셋의 특징에 맞게 클러스터의 개수(nlist)를 설정합니다.
- 훈련 데이터를 사용하여 클러스터를 학습합니다.
- 학습된 클러스터에 벡터를 추가합니다.
검색 방식
- 쿼리 벡터를 입력합니다.
- 쿼리하도록 설정된 클러스터 수(nprobe)에 따라, 쿼리와 가장 가까운 클러스터를 식별합니다.
- 선택된 클러스터 내에서만 검색하여 근사치를 반환합니다.
특징
- 장점: 검색 속도가 빠르고, 대규모 데이터셋에서도 효율적으로 작동합니다. 검색 성능과 메모리 사용량 간의 균형을 유지합니다.
- 단점: 클러스터의 수와 데이터 분포에 따라 정확도가 영향을 받을 수 있으며, 최적화를 위해 추가적인 학습 과정이 필요합니다.
- 적합한 경우: 중대규모 데이터셋에서 빠른 검색이 필요한 경우.
Faiss에서
https://github.com/facebookresearch/faiss/wiki/Faiss-indexes#cell-probe-methods-indexivf-indexes
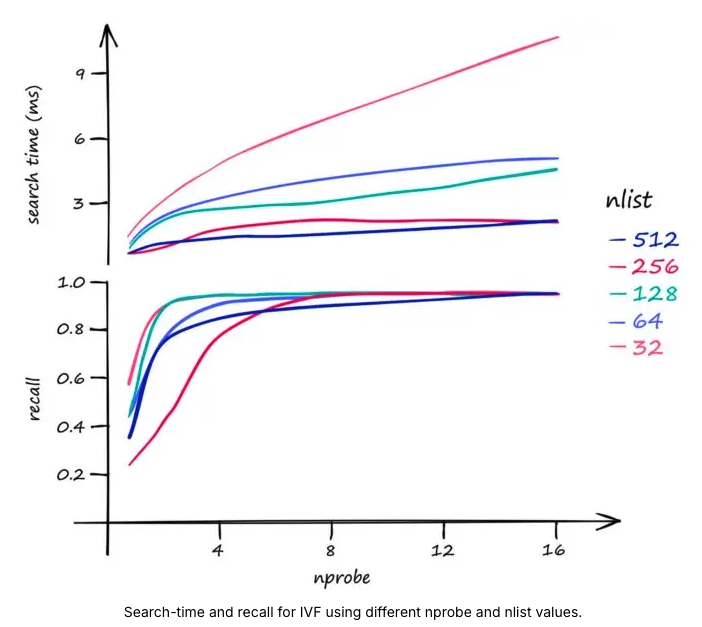
- 검색 속도를 우선시 → nlist를 늘립니다.
- 검색 품질이 우선시 → nprobe를 늘리면 검색 범위가 늘어나 됩니다.
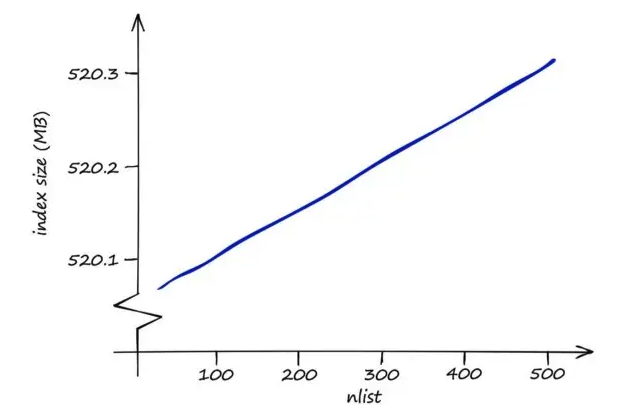
- 메모리 측면에서 IndexIVFFlat은 상당히 효율적이며 nprobe를 수정해도 영향을 미치지 않습니다.
- nlist가 메모리 사용에 미치는 영향도 작습니다. nlist가 높을수록 메모리 요구 사항이 약간 더 커집니다.
Milvus에서
https://milvus.io/docs/index.md?tab=floating#IVFFLAT
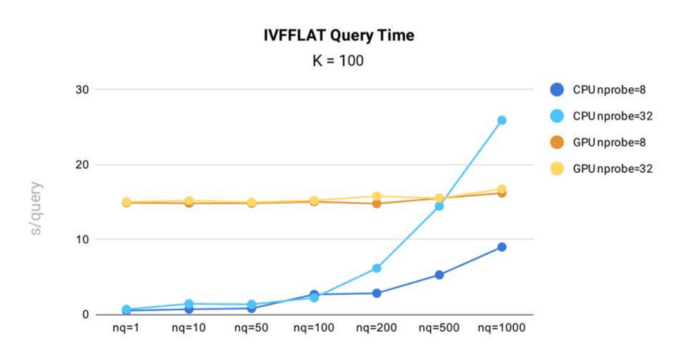
- CPU에서 실행할 때, Milvus의 IVF_FLAT 인덱스의 쿼리 시간은 nprobe와 nq가 증가함에 따라 늘어납니다. 이는 검색할 벡터(nq)가 많아질수록, 혹은 쿼리가 검색하는 클러스터 수(nprobe)가 많아질수록 쿼리 시간이 더 오래 걸린다는 것을 의미합니다.
- GPU에서 해당 인덱스는 nq와 nprobe 변화에 따른 시간 변동이 비교적 적습니다. 이는 인덱스 데이터 크기가 크고, CPU 메모리에서 GPU 메모리로 데이터를 복사하는 작업이 전체 쿼리 시간의 대부분을 차지하기 때문입니다. 모든 시나리오에서, nq = 1,000이고 nprobe = 32인 경우를 제외하면, IVF_FLAT 인덱스는 CPU에서 실행할 때 더 효율적입니다.
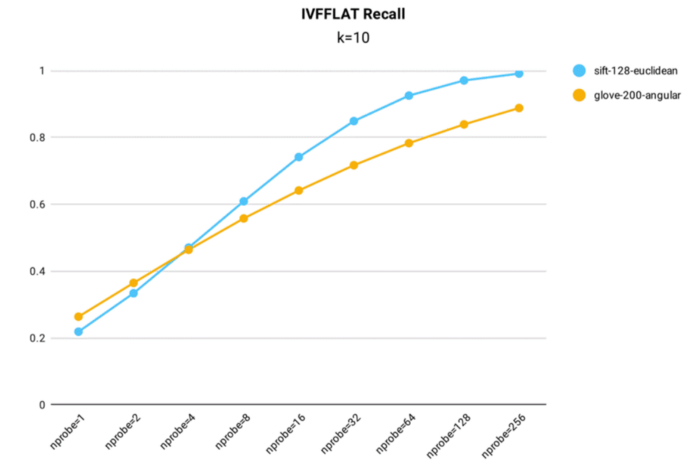
- IVF_FLAT 인덱스는 정확도를 위해 최적화될 수 있으며, nprobe = 256일 때 1M SIFT 데이터 세트에서 0.99 이상의 Recall을 달성할 수 있습니다.
양자화 기법들
벡터 검색에서 메모리를 절약하고 효율성을 높이기 위해 여러 양자화(Quantization) 기술이 사용됩니다. 여기서는 Scalar Quantizer(SQ), Product Quantizer(PQ), Pseudo Residual Quantizer(PRQ)에 대해 살펴봅니다.
Scalar Quantizer (SQ)
- 특징: 각 벡터의 개별 차원을 독립적으로 양자화하여 저장합니다.
- 장점: 구현이 간단하며, 저장 공간을 줄이는 데 효과적입니다.
- 단점: 각 차원을 독립적으로 처리하기 때문에 상호 의존성을 고려하지 못해 정확도가 떨어질 수 있습니다.
Product Quantizer (PQ)
- 특징: 벡터를 서브벡터로 분할한 후 각 서브벡터를 독립적으로 양자화합니다.
- 장점: 대규모 데이터셋에서 효율적인 검색이 가능하며, 메모리 사용량이 낮습니다.
- 단점: 벡터 분할과 양자화 과정에서 정보 손실이 발생할 수 있습니다.
양자화 과정

- 크고, 고차원 벡터를 같은 사이즈의 chunk로 자릅니다 (subvectors)
- 이러한 각 하위 벡터를 가장 가까운 centroid(reproduction/reconstruction 값이라고도 함)에 할당합니다.
- 이러한 centroid 값을 고유 ID로 교체합니다. 각 ID는 centroid을 나타냅니다.
Pseudo Residual Quantizer (PRQ)
- 특징: PQ의 확장으로, 잔여 오차를 양자화하여 정확도를 높이는 방법입니다.
- 장점: PQ보다 높은 정확도를 제공하며, 잔여 오차를 효과적으로 보정합니다.
- 단점: 추가적인 계산과 저장 공간이 필요합니다.
'AI > 검색 시스템' 카테고리의 다른 글
| 검색 시스템을 위한 Document Splitting (1) | 2025.01.26 |
|---|---|
| ANN(Approximate Nearest Neighbor) 알고리즘의 이해 #3 DiskANN (0) | 2025.01.26 |
| ANN(Approximate Nearest Neighbor) 알고리즘의 이해 #1 (0) | 2025.01.26 |
| Retrieval 시스템을 위한 MTEB 벤치마크 (2) | 2025.01.03 |
| Retrieval 시스템을 위한 BEIR 벤치마크 (2) | 2025.01.03 |